Using Linear Regression to Predict House Sale Prices

I interpret linear regression results to determine features that significantly affect house sale prices. I then use the same model to predict house prices, and evaluate the model using stratified k-fold cross-validation.
python
pandas
seaborn
matplotlib
sklearn
statsmodels
Author

Migs Germar

Published

December 28, 2021

Unsplash | Breno Assis

Introduction

The Ames, Iowa housing dataset was formed by De Cock in 2011 as a high-quality dataset for regression projects. It contains data on 80 features of 2930 houses. The target variable is the sale price of each house.

In order to predict the target, I will use linear regression for both statistical inference and machine learning. To each feature (or independent variable), the model will assign a coefficient that shows how the feature affects the target (or dependent variable). I will use the model’s \(p\) values to determine the features with statistically significant effects, then use these features in our final model for predicting prices from new data.

Note

I wrote this notebook by following a guided project on the Dataquest platform, specifically the Guided Project: Predicting House Sale Prices. The general project flow and research questions were guided by Dataquest. Other than what was instructed, I also added my own steps. You can visit the official solution to compare it to my project.

Below are the packages used in this project.

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sms
from sklearn.linear_model import LinearRegression

# Import custom modules that I wrote.
from custom_modules import linreg_tools as lrt, stratified_kfcv as skf

Note that some of the imported modules are custom ones that I wrote. To view these modules, visit this directory in my website’s repository.

Data Inspection and Cleaning

The journal article that introduced the Ames, Iowa housing dataset is linked here. You may click the “PDF” button on the webpage to access the article, which contains the links to download the data file.

A summary of the columns and their data types is shown below.

Code 
houses = pd.read_excel("./private/Linear-Regression-House-Prices-Files/AmesHousing.xls")

houses.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2930 entries, 0 to 2929
Data columns (total 82 columns):
 #   Column           Non-Null Count  Dtype  
---  ------           --------------  -----  
 0   Order            2930 non-null   int64  
 1   PID              2930 non-null   int64  
 2   MS SubClass      2930 non-null   int64  
 3   MS Zoning        2930 non-null   object 
 4   Lot Frontage     2440 non-null   float64
 5   Lot Area         2930 non-null   int64  
 6   Street           2930 non-null   object 
 7   Alley            198 non-null    object 
 8   Lot Shape        2930 non-null   object 
 9   Land Contour     2930 non-null   object 
 10  Utilities        2930 non-null   object 
 11  Lot Config       2930 non-null   object 
 12  Land Slope       2930 non-null   object 
 13  Neighborhood     2930 non-null   object 
 14  Condition 1      2930 non-null   object 
 15  Condition 2      2930 non-null   object 
 16  Bldg Type        2930 non-null   object 
 17  House Style      2930 non-null   object 
 18  Overall Qual     2930 non-null   int64  
 19  Overall Cond     2930 non-null   int64  
 20  Year Built       2930 non-null   int64  
 21  Year Remod/Add   2930 non-null   int64  
 22  Roof Style       2930 non-null   object 
 23  Roof Matl        2930 non-null   object 
 24  Exterior 1st     2930 non-null   object 
 25  Exterior 2nd     2930 non-null   object 
 26  Mas Vnr Type     2907 non-null   object 
 27  Mas Vnr Area     2907 non-null   float64
 28  Exter Qual       2930 non-null   object 
 29  Exter Cond       2930 non-null   object 
 30  Foundation       2930 non-null   object 
 31  Bsmt Qual        2850 non-null   object 
 32  Bsmt Cond        2850 non-null   object 
 33  Bsmt Exposure    2847 non-null   object 
 34  BsmtFin Type 1   2850 non-null   object 
 35  BsmtFin SF 1     2929 non-null   float64
 36  BsmtFin Type 2   2849 non-null   object 
 37  BsmtFin SF 2     2929 non-null   float64
 38  Bsmt Unf SF      2929 non-null   float64
 39  Total Bsmt SF    2929 non-null   float64
 40  Heating          2930 non-null   object 
 41  Heating QC       2930 non-null   object 
 42  Central Air      2930 non-null   object 
 43  Electrical       2929 non-null   object 
 44  1st Flr SF       2930 non-null   int64  
 45  2nd Flr SF       2930 non-null   int64  
 46  Low Qual Fin SF  2930 non-null   int64  
 47  Gr Liv Area      2930 non-null   int64  
 48  Bsmt Full Bath   2928 non-null   float64
 49  Bsmt Half Bath   2928 non-null   float64
 50  Full Bath        2930 non-null   int64  
 51  Half Bath        2930 non-null   int64  
 52  Bedroom AbvGr    2930 non-null   int64  
 53  Kitchen AbvGr    2930 non-null   int64  
 54  Kitchen Qual     2930 non-null   object 
 55  TotRms AbvGrd    2930 non-null   int64  
 56  Functional       2930 non-null   object 
 57  Fireplaces       2930 non-null   int64  
 58  Fireplace Qu     1508 non-null   object 
 59  Garage Type      2773 non-null   object 
 60  Garage Yr Blt    2771 non-null   float64
 61  Garage Finish    2771 non-null   object 
 62  Garage Cars      2929 non-null   float64
 63  Garage Area      2929 non-null   float64
 64  Garage Qual      2771 non-null   object 
 65  Garage Cond      2771 non-null   object 
 66  Paved Drive      2930 non-null   object 
 67  Wood Deck SF     2930 non-null   int64  
 68  Open Porch SF    2930 non-null   int64  
 69  Enclosed Porch   2930 non-null   int64  
 70  3Ssn Porch       2930 non-null   int64  
 71  Screen Porch     2930 non-null   int64  
 72  Pool Area        2930 non-null   int64  
 73  Pool QC          13 non-null     object 
 74  Fence            572 non-null    object 
 75  Misc Feature     106 non-null    object 
 76  Misc Val         2930 non-null   int64  
 77  Mo Sold          2930 non-null   int64  
 78  Yr Sold          2930 non-null   int64  
 79  Sale Type        2930 non-null   object 
 80  Sale Condition   2930 non-null   object 
 81  SalePrice        2930 non-null   int64  
dtypes: float64(11), int64(28), object(43)
memory usage: 1.8+ MB

The output above shows the name of each column, its number of non-null values, and its data type. Most of the names are self-explanatory, but others are not so clear. One can visit the data documentation to learn what each column represents.

Here are the first steps I took in order to clean these columns:

  • Based on a suggestion in page 4 of De Cock (2011), I deleted 5 outlier observations which had above-ground living areas higher than 4000 square feet.
  • I selected 9 useful numeric/ordinal columns and 2 useful categorical columns based on their descriptions in the data documentation.
  • I transformed the Overall Qual and Overall Cond columns. Originally, these contained integers from 1 to 10, which represented ordinal ratings from Very Poor to Very Excellent. I put these ratings into 4 groups:
    • 1 represents Very Poor to Fair
    • 2 represents Below Average to Above Average
    • 3 represents Good and Very Good
    • 4 represents Excellent and Very Excellent
  • I inspected the missing values in my final set of columns.
Code 
# Remove outliers based on suggestion in journal article
houses = houses.loc[houses["Gr Liv Area"] < 4000]

# Identify important columns
useful_numerics = [
    "Lot Frontage",
    "Lot Area",
    "Mas Vnr Area",
    "Total Bsmt SF",
    "Gr Liv Area",
    "Fireplaces",
    "Garage Area",
    # The 2 below are ordinal.
    "Overall Qual",
    "Overall Cond",
]

useful_categoricals = [
    "Lot Config",
    "Bldg Type",
]

target_col = "SalePrice"

# Keep only the important columns
houses = houses.loc[:, useful_numerics + useful_categoricals + [target_col]]

ratings_simplified = {
    10: 4,
    9: 4,
    8: 3,
    7: 3,
    6: 2,
    5: 2,
    4: 2,
    3: 1,
    2: 1,
    1: 1,
}

# Replace integers in these two columns with a new set of integers
for col in ["Overall Qual", "Overall Cond"]:
    houses[col] = houses[col].replace(ratings_simplified)

houses.isnull().sum() / houses.shape[0] * 100
Lot Frontage     16.752137
Lot Area          0.000000
Mas Vnr Area      0.786325
Total Bsmt SF     0.034188
Gr Liv Area       0.000000
Fireplaces        0.000000
Garage Area       0.034188
Overall Qual      0.000000
Overall Cond      0.000000
Lot Config        0.000000
Bldg Type         0.000000
SalePrice         0.000000
dtype: float64

The table above shows the percentage of missing values in each column. Most columns have less than 1% missingness, but the Lot Frontage column has almost 17% missingness. This is higher than my preferred benchmark of 5% missingness, so I will remove the Lot Frontage column.

After deleting that column, I will remove rows where there are any remaining missing values.

Code 
houses = houses.drop("Lot Frontage", axis = 1).dropna()

print(f"Total number of missing values: {houses.isnull().sum().sum()}")
print(f"New shape: {houses.shape}")
Total number of missing values: 0
New shape: (2900, 11)

Now, the dataset has 2900 rows and 11 columns, including 10 features and 1 target.

Next, two of my features are categorical. Thus, in order to use them in regression, I have to dummy code them. According to the UCLA: Statistical Consulting Group (2021), if there are \(k\) categories in one variable, I must make \(k - 1\) new variables containing zeroes and ones. The reason that only \(k - 1\) variables are made is that one category has to be set aside as the “reference level.” The other categories will be compared to the reference level when I fit the model.

In Python, I will do this using the pd.get_dummies() function. I will set the drop_first parameter to True so that one category will be excluded from the final variables.

Code 
cat_features = ["Lot Config", "Bldg Type"]

houses = houses.merge(
    pd.get_dummies(houses[cat_features], drop_first = True),
    left_index = True,
    right_index = True,
    how = "outer",
)

houses = houses.drop(cat_features, axis = 1)

(
    houses
    .loc[:, houses.columns.to_series().str.match(r"Lot Config|Bldg Type")]
    .head()
)
Lot Config_CulDSac Lot Config_FR2 Lot Config_FR3 Lot Config_Inside Bldg Type_2fmCon Bldg Type_Duplex Bldg Type_Twnhs Bldg Type_TwnhsE
0 0 0 0 0 0 0 0 0
1 0 0 0 1 0 0 0 0
2 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0
4 0 0 0 1 0 0 0 0

The table above shows the first 5 rows of the new variables that were created. Since there were 5 categories in the Lot Config variable, 4 new variables were created. This is also the case for the Bldg Type variable.

Let’s take the first column, Lot Config_CulDSac, as an example. It represents houses that are situated on a cul-de-sac. A house with a value of 1 in this column is a house on a cul-de-sac. Other houses, with values of 0, are not.

The data is clean now, so I can proceed to statistical inference.

Statistical Inference

In this section, I will fit an Ordinary least Squares (OLS) linear regression model. Then, I will check the assumptions of linear regression in order to make sure that this is the right model for the problem. I will also use the results of the model to select the best features.

The code below fits the OLS model and outputs the first of three tables of results. I will interpret the results based on what I learned from the article “Linear Regression” by Python for Data Science (n.d.).

Code 
feature_cols = [x for x in houses.columns if x != target_col]

# Add a constant column in the dataset so that the model can find the y-intercept.
X = sms.add_constant(
    houses[feature_cols]
)
y = houses[target_col]

# Obtain Variance Inflation Factors.
vif_df = lrt.get_vif(X)

model = sms.OLS(y, X)
results = model.fit()
summary = results.summary()

tables = lrt.extract_summary(summary, vif_df)

tables[0]
C:\Users\migs\anaconda3\envs\new_streamlit_env2\lib\site-packages\statsmodels\tsa\tsatools.py:142: FutureWarning: In a future version of pandas all arguments of concat except for the argument 'objs' will be keyword-only
  x = pd.concat(x[::order], 1)
0 1 2 3
0 Dep. Variable: SalePrice R-squared: 0.838
1 Model: OLS Adj. R-squared: 0.837
2 Method: Least Squares F-statistic: 929.200
3 Date: Fri, 14 Jan 2022 Prob (F-statistic): 0.000
4 Time: 14:44:14 Log-Likelihood: -34163.000
5 No. Observations: 2900 AIC: 68360.000
6 Df Residuals: 2883 BIC: 68460.000
7 Df Model: 16 NaN NaN
8 Covariance Type: nonrobust NaN NaN

This first table shows two important things. The R-squared value is equal to 0.838, meaning that the model explained 83.8% of the variance in the data. Ideally, I would want a value close to 100% but this is good. Also, the p value of the F-statistic is equal to 0. Since \(p < 0.05\), the model was statistically significant overall.

Next, below is the second table of results.

Code 
tables[1]
coef std err t P>|t| [0.025 0.975] VIF
feature
const -105800.0000 4319.486 -24.498 0.000 -114000.000 -97400.000 53.813031
Lot Area 0.5717 0.084 6.789 0.000 0.407 0.737 1.243636
Mas Vnr Area 49.6396 3.863 12.849 0.000 42.065 57.214 1.334007
Total Bsmt SF 40.8966 1.780 22.979 0.000 37.407 44.386 1.618427
Gr Liv Area 48.9365 1.660 29.481 0.000 45.682 52.191 1.883476
Fireplaces 7000.7868 1069.148 6.548 0.000 4904.416 9097.158 1.373267
Garage Area 53.8240 3.528 15.256 0.000 46.906 60.742 1.643206
Overall Qual 44530.0000 1344.831 33.113 0.000 41900.000 47200.000 1.924753
Overall Cond 9206.0505 1269.656 7.251 0.000 6716.526 11700.000 1.056642
Lot Config_CulDSac 14770.0000 2804.614 5.265 0.000 9266.896 20300.000 1.307018
Lot Config_FR2 371.8734 3776.296 0.098 0.922 -7032.639 7776.385 1.156834
Lot Config_FR3 8290.0511 8929.437 0.928 0.353 -9218.674 25800.000 1.026279
Lot Config_Inside 4695.2344 1586.888 2.959 0.003 1583.685 7806.784 1.425754
Bldg Type_2fmCon -21140.0000 4144.743 -5.100 0.000 -29300.000 -13000.000 1.036636
Bldg Type_Duplex -24340.0000 3214.492 -7.572 0.000 -30600.000 -18000.000 1.078048
Bldg Type_Twnhs -9050.9650 3363.564 -2.691 0.007 -15600.000 -2455.731 1.096859
Bldg Type_TwnhsE 3408.7248 2328.503 1.464 0.143 -1156.975 7974.425 1.146414

Each row other than the constant row represents a feature.

The coef column gives the increase in the target for a one-unit increase in the feature (Frost, 2017). For example, the coefficient of Gr Liv Area (above-ground living area in square feet) is around 49. Therefore, for every 1 square foot increase in living area, the sale price increases by USD 49.

According to UCLA: Statistical Consulting Group (2021), the coefficient of a dummy-coded variable gives the difference between the mean of the target for the level of interest and the mean of the target for the reference level. For example, the coefficient of Lot Config_CulDSac is 14,770. Therefore, the price of a house on a cul-de-sac is usually USD 14,770 higher than that of a house on a corner lot.

The P>|t| column gives the p value of each feature. A p value less than 0.05 can be considered statistically significant, whereas a p value above that threshold is not. In the case of this model, most of the features are statistically significant.

The insignificant features are Lot Config_FR2 (houses with frontage on 2 sides), Lot Config_FR3, and Bldg Type_TwnhsE (Townhouse End Units). Though these are not significant, I will keep them in the model because they are necessary components of the dummy-coded categorical variables.

Next, the VIF column contains Variance Inflation Factors. I wrote code to calculate these values based on an article, “Detecting Multicollinearity with VIF – Python,” by cosine1509 (2020).

According to Frost (2017), VIFs are a measure of multicollinearity among independent variables. The lowest possible value is 1, which means no collinearity at all. Values between 1 and 5 show low to moderate multicollinearity, so these are acceptable. However, values over 5 show high multicollinearity and need to be investigated.

In the case of this model, all of the VIFs of the features are below 2. The VIF of the constant term is high, but this is not important.

In summary, based on the p values and VIF values, there is no need to change the features used in the model. Most of them are significant, and all of them have low multicollinearity.

Finally, let us look at the third table of results.

Code 
tables[2]
0 1 2 3
0 Omnibus: 421.519 Durbin-Watson: 1.583
1 Prob(Omnibus): 0.000 Jarque-Bera (JB): 3490.274
2 Skew: 0.426 Prob(JB): 0.000
3 Kurtosis: 8.307 Cond. No. 195000.000

The Durbin-Watson test statistic is 1.583. According to Python for Data Science (n.d.), this statistic should ideally be close to 2. If it is below 2, there is positive autocorrelation among the residuals, so one of the assumptions of linear regression is violated. However, as a rule of thumb, values between 1.5 and 2.5 are acceptable. Thus, this statistic is not a cause of concern.

On the other hand, the Jarque-Bera p value is 0. Because \(p < 0.05\), the statistic is significant, so the residuals are not distributed normally. However, Mordkoff (2016) says that according to the Central Limit Theorem, “as long as the sample is based on 30 or more observations, the sampling distribution of the mean can be safely assumed to be normal.” Therefore, this is fine.

That’s it for the statistical inference part of this project. Now that I know that my variables are statistically significant, I can make a predictive model and evaluate it.

Predictive Modeling and Evaluation

In this last part, I will use scikit-learn to fit a linear regression model for prediction. A 5-fold cross-validation will be used in order to evaluate the model.

In my recent project about the KNN model, I wrote some custom functions that help perform stratified cross-validation. This means that the folds are divided such that each fold’s target distribution (in this case, price distribution) is similar to that of the full sample. I put the custom functions in the stratified_kfcv file, which can be found here for your reference.

I performed stratified 5-fold cross-validation on the housing data, so 5 models were fitted and their RMSEs were recorded. The results are shown below.

Code 
fold_series = skf.stratify_continuous(
    n_folds = 5,
    y = houses["SalePrice"],
)

lr = LinearRegression()

mse_lst = skf.stratified_kfcv(
    X = sms.add_constant(houses[feature_cols]),
    y = houses[target_col],
    fold_series = fold_series,
    regression_model = lr,
)

rmses = pd.Series(mse_lst).pow(1/2)

print(f"""RMSE Values:
{rmses}
Mean RMSE: {rmses.mean()}
SD RMSE: {rmses.std(ddof = 1)}""")
RMSE Values:
0    32046.873780
1    30927.932397
2    30637.750905
3    33020.953872
4    32832.216461
dtype: float64
Mean RMSE: 31893.145482987817
SD RMSE: 1082.253470974206
C:\Users\migs\anaconda3\envs\new_streamlit_env2\lib\site-packages\statsmodels\tsa\tsatools.py:142: FutureWarning: In a future version of pandas all arguments of concat except for the argument 'objs' will be keyword-only
  x = pd.concat(x[::order], 1)

The mean RMSE is 31,893. Therefore, the predicted prices are usually USD 31,893 away from the true prices. Also, the standard deviation RMSE is around 1082, so the RMSE values were relatively consistent from test to test.

The mean RMSE may seem high, but remember the distribution of house prices in the dataset:

Code 
sns.histplot(
    data = houses,
    x = "SalePrice"
)

plt.title("Distribution of House Sale Prices")
plt.xlabel("Sale Price (USD)")
plt.show()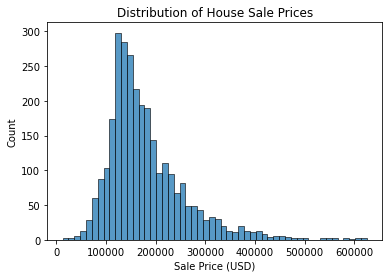

The prices are mostly around USD 100,000 to USD 300,000. Thus, the mean RMSE is relatively small considering the prices. Therefore, I would say that the model performs decently, but it could be improved.

Conclusion

In this project, I cleaned data about houses in Ames, Iowa, selected features that may be useful, interpreted linear regression results to determine significant features, then evaluated a predictive model. I found that the 16 independent variables explained 83.8% of the variance \((R^2 = 0.838, F(16, 2883 = 929.2), p < 0.05)\). Furthermore, the predictive model had a mean RMSE of 31,880, which was decent but not ideal.

Thanks for reading!

Bibliography

Data Source

De Cock, D. (2011). Ames, Iowa: Alternative to the Boston Housing Data as an End of Semester Regression Project. Journal of Statistics Education, 19(3), null. https://doi.org/10.1080/10691898.2011.11889627

Information Sources

Coding Systems for Categorical Variables in Regression Analysis. (n.d.). UCLA: Statistical Consulting Group. Retrieved December 26, 2020, from https://stats.idre.ucla.edu/spss/faq/coding-systems-for-categorical-variables-in-regression-analysis-2/

cosine1509. (2020, August 14). Detecting Multicollinearity with VIF - Python. GeeksforGeeks. https://www.geeksforgeeks.org/detecting-multicollinearity-with-vif-python/

Frost, J. (2017a, April 2). Multicollinearity in Regression Analysis: Problems, Detection, and Solutions. Statistics By Jim. http://statisticsbyjim.com/regression/multicollinearity-in-regression-analysis/

Frost, J. (2017b, April 12). How to Interpret P-values and Coefficients in Regression Analysis. Statistics By Jim. http://statisticsbyjim.com/regression/interpret-coefficients-p-values-regression/

Mordkoff, J. T. (2016). The Assumption(s) of Normality. http://www2.psychology.uiowa.edu/faculty/mordkoff/GradStats/part%201/I.07%20normal.pdf

Python for Data Science. (2018, March 15). Linear Regression. Python for Data Science. https://pythonfordatascienceorg.wordpress.com/linear-regression-python/

Image Source

Assis, B. (2018, January 17). Photo by Breno Assis on Unsplash. Unsplash. https://unsplash.com/photos/r3WAWU5Fi5Q